In 1990 image processing in general and image recognition in particular was still in early stages of development. I was at the NTT Basic Research Laboratory in Musashino, Japan for a post-doctoral position, and ran across a technique known as singular value decomposition (SVD).

SVD was not so new to mathematics, but it surprised me that with all my control systems background at M.I.T., I had never seen it before. What really interested me then, and still fascinates me is the ability of SVD to capture the variability in a data set, and reduce the dimensionality of a problem in a formalized way, and to a specified level of precision.

In 1990 the computers were still not so fast, so computation seemed expensive. I was intrigued by the idea of taking a set of images, which consists of, say, 10⁵ pixels, and using SVD to find a space of, say 30 dimensions which capture most of the variability, and doing pattern matching in the reduced space of 30 dimensions rather than the original space of 10⁵ !

Each image is a point, together they form a manifold.

The problem arose that to compute the SVD would normally require multiplying images by each other, or 10⁵ * N² multiplications for N images. My notes indicate that top-of-the-line computers of that time had a grand total of 8 MB of virtual memory!

I realized that by using run-length-encoding of quantized images, I could reduce the computational problem by a factor of 100 or so, and make it feasible again. I also developed a couple other techniques to deal with the relatively large data sets involved, and was able to compute eigenvalues for various sets of images, and try to extract unknown parameters based on the reduced-dimensionality space.

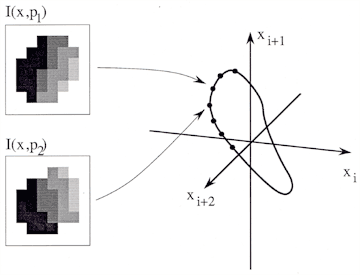
The first set of images I tried working with was rotations of a capsule-like geometric shape. I created a set of images for which I knew the rotational parameters, then computed the SVD using my technique. Then I could compute take images with unknown parameters, and try to estimate the parameters in the subspace. 99

Two of the calibration images.

Four of the eigenvalues computed from the calibration set.

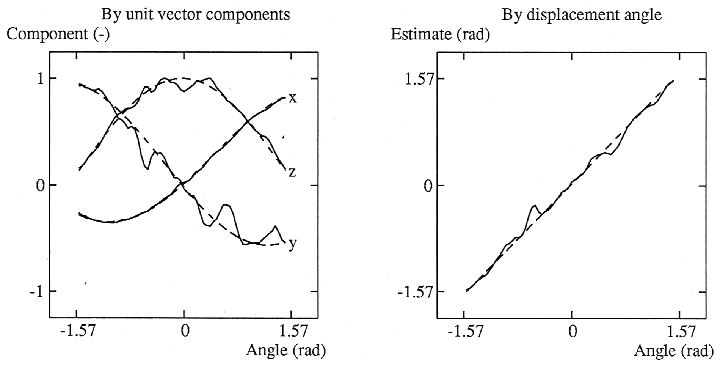
By varying the signal to noise ratio of the input images, I was able to characterize the ability of the method at measuring parameters from image data.

Graph of exact, and measured unkown parameters for various samples.

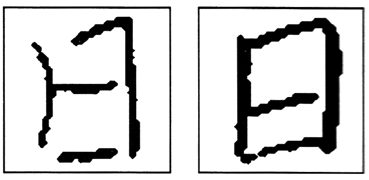
My colleagues Hiroshi Murase went on to extend the work for kanji characters. In our paper, we presented eigenvectors derived from various images, such as the hand-written kanji which produces the eigenvectors shown below.

Two of the input medium complexity sample set.

Four of the eigenvalues computed from the medium complexity set.

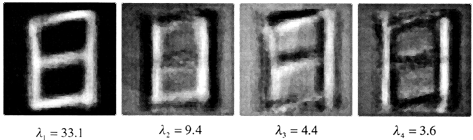I believe this general technique has not yet been fully exploited, and there are still applications in image processing that can make use of it.